Vision
Research in the Cognitive NeuroSystems Lab includes work on vision: how our eyes and brain work together to help us see.
The focus has been on color vision and the visual system's use of image spectral information as seen through the cone photoreceptors.
Can the colors we see be understood in terms of neural mechanisms found in eye and brain? There are some who say that
color is determined by the wavelengths of the lights that reach the eye. For example, longer wavelength lights tend to appear redder,
shorter wavelength lights bluer, etc. Yet the view taken in this work is that there is no color unless there is
somebody there to perceive it. Although an object may provide chromatic information through the wavelength constitution
of the lights that it reflects towards the eye, its color exists only in the mind of the beholder. Current work is focused on using chromatic, border ownership and depth information to help segment images.
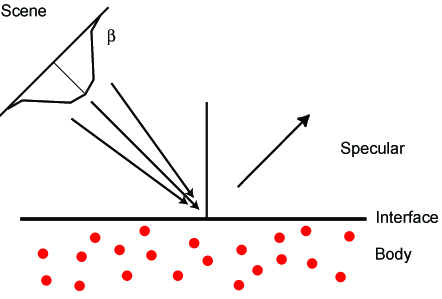 |
Color constancy If we change the light that shines on a surface, the light reflected by the surface towards the eye can change dramatically. Yet under many circumstances the surface continues to appear the same color. This stability of surface color is known as color constancy. Color constancy is possible if the visual system is sensitive to information about the spectral properties of surface reflectance and scene illumination. What is this information and how is it used? Peter Lennie and D'Zmura showed in early work that specular highlights provide information about the spectral properties of a light source. At left is shown a diagram indicating that the image received from a shiny surface is a composite of not only diffusely-reflected light contributed pigment molecules (body) but also a blurred version of the surrounding scene (specular). We also argued that the hue of an object is roughly independent of its shape and position. We showed how specular highlight information can be used to infer object reflectance properties, using linear models of illumination and reflectance spectral power distributions. While these physical reflectance properties vary from surface to surface, they do not depend on scene illumination; surface reflectance information is color constant. Geoff Iverson and D'Zmura performed a detailed examination of the information available when one or more objects is lit by one or more light sources. The result is that the change in chromatic information from surfaces caused by a change in the spectral properties of the light source provides enough information for a visual system to recover surface reflectance information, under quite general conditions. Such changes in light source properties can occur across time (noon vs. dusk) or as a function of position (directly lit vs. in shadow). |
D'Zmura, M. & Lennie, P. (1986). Mechanisms of color constancy. Journal of the Optical Society of America A 3, 1662-1672. [PDF]
D'Zmura, M. (1992). Color constancy: surface color from changing illumination. Journal of the Optical Society of America A 9, 490-493. [PDF]
D'Zmura, M. & Iverson, G. (1992). Color constancy: adaptation to the illumination environment. Optical Society of America Topical Meeting on Advances in Color Vision Technical Digest, 107-109.
D'Zmura, M. & Iverson, G. (1993). Color constancy. I. Basic theory of two-stage linear recovery of spectral descriptions for lights and surfaces. Journal of the Optical Society of America A 10, 2148-2165.
[PDF]
D'Zmura, M. & Iverson, G. (1993). Color constancy. II. Results for two-stage linear recovery of spectral descriptions for lights and surfaces. Journal of the Optical Society of America A 10, 2166-2180. [PDF]
D'Zmura, M. & Iverson, G. (1994). Color constancy. III. General linear recovery of spectral descriptions for lights and surfaces. Journal of the Optical Society of America A 11, 2389-2400. [PDF]
Iverson, G. & D'Zmura, M. (1994). Criteria for color constancy in trichromatic bilinear models. Journal of the Optical Society of America A 11, 1970-1975. [PDF]
D'Zmura, M., Iverson, G. & Singer, B. (1995). Probabilistic color constancy. In Luce, R.D., D'Zmura, M., Hoffman, D.D., Iverson, G. and Romney, K. (Eds.), Geometric Representations of Perceptual Phenomena. Mahwah, NJ: Lawrence Erlbaum Associates, 187-202.
Iverson, G. & D'Zmura, M. (1995). Color constancy: spectral recovery using trichromatic bilinear models. In Luce, R.D., D'Zmura, M., Hoffman, D.D., Iverson, G. and Romney, K. (Eds.), Geometric Representations of Perceptual Phenomena. Mahwah, NJ: Lawrence Erlbaum Associates, 169-185.
D'Zmura, M. & Iverson, G. (1998). A formal approach to color constancy: the recovery of surface and light source spectral properties using bilinear models. In Dowling, C., Roberts, F. and Theuns, P. (Eds.) Recent Progress in Mathematical Psychology. Mahwah, NJ: Lawrence Erlbaum Associates, 99-132.
 |
Contrast gain control Ben Singer and D'Zmura investigated properties of visual contrast gain control in experiments on chromatic contrast induction. A first property is that contrast induction is chromatically selective. As shown at left, a black-white disk appears to have lesser contrast in the presence of a high-contrast black-white surround (top left) than in the presence of a red-green surround (top middle) or a blue-yellow surround (top right). Likewise, the apparent contrast of a red-green disk is suppressed most strongly by a red-green surround (bottom middle); apparent contrast suppression is less when the red-green disk is surrounded by black-white (bottom left) or blue-yellow (bottom right) patterns. Further properties determined experimentally include a sluggish temporal sensitivity to contrast modulation, a broad spatial sensitivity, and a binocular (cortical) locus. These were built into a feedforward model of contrast gain control, based on the idea that the signal of a neuron, sensitive to contrast in some central image region, is controlled in a feedforward fashion by inhibitory signals concerning contrast from a larger surrounding area. Much of this work is described in the doctoral dissertation of Ben Singer. The contrast suppression of central disks like those shown at left often appears to involve transparency; this observation led to work on transparency described below. |
Singer, B. & D'Zmura, M. (1994). Color contrast induction. Vision Research 34, 3111-3126. [PDF]
Singer, B. & D'Zmura, M. (1995). Contrast gain control. A bilinear model for chromatic selectivity. Journal of the Optical Society of America A, 12, 667-685.
[PDF]
D'Zmura, M. & Singer, B. (1996). The spatial pooling of contrast in contrast gain control. Journal of the Optical Society of America A, 13, 2135-2140.
[PDF]
D'Zmura, M. (1997). Neural network for color contrast gain control. Proceedings of the European Symposium on Artificial Neural Networks, Bruges, Belgium, April 1997, pp. 67-72.
D'Zmura, M. (1998). Color contrast gain control. In Backhaus, W., Kliegl, R. & Werner, J. (Eds.) Color Vision. Berlin: Walter de Gruyter, 251-266.
D'Zmura, M. & Singer, B. (1999) Contrast gain control. In Sharpe, L.T. & Gegenfurtner, K.R. (Eds.) Color Vision: From Genes to Perception. Cambridge: Cambridge University Press, 369-385.
 |
Detection and visual search A fundamental question in color vision research concerns the organization of neurons which are sensitive to chromatic information. Do we have neurons for each possible color in the spectrum or do we have neurons for only some small set of colors like red, yellow, green and blue? How sensitive is such a neuron to similar, neighboring colors? Early work using a visual search paradigm suggested that we have neurons tuned to a wide variety of hues. This work suggested also that these neurons have very broad sensitivities. A neuron tuned to orange will also respond to neighboring colors like red and yellow. Indeed, the sensitivities measured in these experiments appeared consistent with a linear combination of photoreceptoral sensitivities. Assuming that chromatically-sensitive neurons used in visual search tasks are tuned to a wide variety of colors and have broad linear sensitivities, one can then use standard signal-detection theory to predict which colors are likely to be found easily when presented among other colors. For example, a single red disk is readily found when presented among a sea of green disks. That same red disk is found less easily when presented among violet and orange disks. More precise measurements of sensitivity are possible using noise masking paradigms. Ken Knoblauch and D'Zmura used sectored noise to measure the bandwidths of chromatic detection mechanisms. As indicated at left, such noise occupies a sector of the color plane. The sector is chosen to be centered on the axis a of a chromatic signal; the width of the sector can be varied. How much the sectored noise masks the detection of the signal along axis a, as a function of sector width, gives one a good idea of the bandwidth of the detection mechanism. We found broad sensitivities that are consistent with the linear combination of photoreceptoral inputs by the detection mechanisms. Further work by Peter Lennie, Carlo Tiana and D'Zmura on visual search showed that visual search may be conducted in parallel with figures defined by mechanisms of figure-ground segregation. |
D'Zmura, M. (1991). Color in visual search. Vision Research 31, 951-966.
[PDF]
D'Zmura, M. & Mangalick, A. (1994). Detection of contrary chromatic change. Journal of the Optical Society of America A 11, 543-546. [PDF]
D'Zmura, M., Lennie, P. & Tiana, C. (1997). Color search and visual field segregation. Perception & Psychophysics 59, 381-388.
D'Zmura, M. & Knoblauch, K. (1998) Spectral bandwidths for the detection of color. Vision Research 38, 3117-3128.
[PDF]
D'Zmura, M., Colantoni, P. & Hagedorn, J. (2001) Perception of color change. Color Research and Application S26, S186-S191.
[PDF]
 |
Transparency How do the colors and lightnesses of surfaces seen to lie behind a transparent filter depend on filter chromatic properties? Ken Knoblauch, Philippe Colantoni, Bernard Laget, Vincent Chen and D'Zmura suggested that the visual system interprets a filter's operation in terms of color space convergence. Such a convergence is described by a color shift and a change in contrast. Karl Gegenfurtner, Oliver Rinner and D'Zmura tested the model using an asymmetric matching task. Observers adjusted, in computer graphic simulation, the color of a surface seen behind a transparent filter in order to match the color of a surface seen in plain view. Although the convergence model fit the color-matching results well, it continued to run into problems with special cases found in the work by Chen and D'Zmura. The math behind the convergence model fits well the physical description of the effects of fog caused by water molecules in the atmosphere. This led John Hagedorn and D'Zmura to study how the colors and lightnesses of surfaces seen through fog depend on fog chromatic properties. A convergence model fit the data well. Ma Ge developed a model to account better for the special cases found in the work by Chen and D'Zmura. Light from a filter comes not only from underlying surfaces but also from light reflected directly by the filter. Recognizing if this filter reflection occurs is easy in cases where the light from the filter area is more intense than that from the surrounding surfaces. Ge's hybrid model of transparency perception operates in different ways depending on filter and surface light levels and is described in his doctoral dissertation. |
D'Zmura, M., Colantoni, P., Knoblauch, K. & Laget, B. (1997). Color transparency. Perception 26, 471-492 [PDF].
Colantoni, P., D'Zmura, M., Knoblauch, K. & Laget, B. (1997) Detection of color transparency. In Rogowitz, B. & Allenbach, J. (Eds.) Human Vision and Electronic Imaging II Vol. 3016, 360-368.
Chen, V.J. & D'Zmura, M. (1998), Test of a convergence model for color transparency perception. Perception 27, 595-608.
Hagedorn, J. & D'Zmura, M. (2000). Color appearance of surfaces viewed through fog. Perception 29, 1169-1184. [PDF]
D'Zmura, M., Rinner, O. & Gegenfurtner, K.R. (2000). The colors seen behind transparent filters. Perception 29, 911-926.
[PDF]
 |
Other The blurring of a scene in the light reflected from a shiny object depends on the microscopic roughness properties of the surface. This variation is captured by computer graphic models for surface reflection. Many such models lead to a simple description of surface reflection properties when described in the frequency domain because they desribe surface reflection as a shift-invariant linear system. The angle between an incident light and the surface normal, the angle between the exiting reflected light and the surface normal, and the direction towards the viewer, are all specified for an opaque shiny surface as directions on the hemisphere above the surface. A frequency domain approach thus involves surface spherical harmonics. These vary in frequency (labelled l at the bottom of the picture at left--often called the degree) and in order (labelled m at the side of the middle panels). At top left is shown a Mercator projection of a spatial noise pattern of incident illumination. Middle left shows the spherical harmonic transform of this input light while at bottom left is shown the power spectrum of the input light. These spectra capture information about how much a particular spherical harmonic of frequency l (horizontal axis) and order m (vertical axis, middle panels) contibutes to a given pattern of light. A simple shift-invariant linear filter can be described completely by a set of numbers used to attenuate, in a frequency-dependent fashion, the power of incident light (center and bottom middle panels). The result of the filtering, shown at right, is a light pattern reflected by the surface. This output pattern is a blurred version of the input incident light pattern. Advancing computer power over the past decades has made this frequency-domain approach more common as a tool in computer graphics and in visual studies of surface perception. |
D'Zmura, M. & Lennie, P. (1986). Shared pathways for rod and cone vision. Vision Research 26, 1273-1280. [PDF]
Lennie, P. & D'Zmura, M. (1988). Mechanisms of color vision. Critical Reviews in Neurobiology 3, 333-400.
D'Zmura, M. (1991). Shading ambiguity: reflectance and illumination. In Computational Models of Visual Processing, Landy, M.S. and Movshon, A.J. (Eds.) Cambridge: MIT, 187-207.
D'Zmura, M., Knoblauch, K., Henaff, M.-A. & Michel, F. (1998) Dependence of color on context in a case of cortical color vision deficiency. Vision Research 38, 3455-3459.
[PDF]
Much of this work on vision was funded by the National Eye Institute of the National Institutes of Health.
Work in 1995-96 was also supported by a Bourse d'Accueil Fellowship from the Region Rhone-Alpes (France) to D'Zmura; work in 1997 was also supported by a Deutsche Akademischer Austauschdienst Scholarship.





